Dynamic Prgoramming
Dynamic Programming (DP) is an algorithmic technique for solving an optimization problem by breaking it down into simpler subproblems and utilizing the fact that the optimal solution to the overall problem depends upon the optimal solution to its subproblems.
It has two characters.
- An original problem’s solution uses the same subproblem multiple times. Subproblems are smaller versions of the original problem.
- An original problem has optimal substructure property. Any problem has optimal substructure property if its overall optimal solution can be constructed from the optimal solutions of its subproblems.
It is often used to solve questions which are getting min/max, the number of ways, and existing or not.
Greedy vs DP vs DFS:
Greedy is based on some heuristic to pick a current optimal solution for a subproblem, and hopefully, the current optimal solution can lead to the final optimal solution. For example, we have 1, 2 , 5 three types of coins. When we want to find 6 dollars change and use less coins as possible, we can use a heuristic as the total is fixed, and the coin’s amount bigger, the less coins needed. First we will find 5 and then we will find 1. 2 is exactly the minimal number of coins. However, if our coins values are 1, 3, 4. Based on our heuristic, we will choose 4, 1, and 1. 3 coins are actually not the optimal solution. If we use 3 and 3, we can find 6 with 2 coins.
DP scans all subproblems by steps, and picks the optimal solution at each step. Each step’s optimal solution leads to the final optimal solution. Its advantage appears when there are overlapping problems.
DFS also scans all subproblems, and pick the optimal solution from all possible subproblems in one step. If there are any overlapping problems, we will scan the overlapping problems multiple times.
We can think of most of questions as a graph. I will draw how each algorithm scan the graph. To display DP’s advantage, we will draw a graph with overlapping nodes.
DFS 是穷举所有从起点到最深点的路径。如果一个子问题无法聚拢(For example, tree), DFS可以穷举所有答案, DP没有任何优势,就是DFS。
如果子问题可以聚拢(For examale, sum, max, min, exit or not, how many ways),多个子问题可以合并就可以用DP。 因为如果子问题有聚拢后又发散的,就会出现重复子问题。

During an interview, if we make some heuristic and it can guide each step’s optimal solution to make the final optimal solution, we will try to use greedy algorithm. Otherwise, we can try to use DP. If the question has no overlapping subproblem, we will use DFS.
BFS vs DP on Shortest Path Problem:
BFS is a modified version of Dijkstra with weight all equal to 1. Dijkstra is a greedy algorithm which can find optimal solution when every weight is positive. DP can always find the shortest path whatever a weight is positive or negative. However it is more complicated. Dijkstra is rarely asked during an interview. Therefore, if we find the weight all equal to 1, we shall try BFS first. Otherwise, we will use DP to find the shortest path.
Technique:
There are 3 steps to find solve a DP problem,
-
First we need to find status and choices. Status is the variables that changes from original problem to subproblem. Choices are the values that lead to status changes.
-
Define recursion functions. The function’s return is often the original problem’s solution. The function’s input are status. We can suppose that we have get all subproblems’ result but not the last step’s. We need to find how we can find the last step’s result by using the former result. The recursion function both work for DFS and DP. The difference is DP will use a DP table to save some middle result.
如果reucrsion function 里,其中一些子问题不仅能组成(更大)下一层子问题的结果,还可以组成同层的答案,那么就说明存在重复子问题,我们应该考虑用DP。For example, If we find the recursion function is as
f(n) = f(n - 1) + c, it is a DFS. There is not an overlapping problem. If the recursion function isf(n) = f(n - 1) + f(n - 2), we can use DP.f(n - 2)can composef(n), at the same time,f(n - 2)can composef(n - 1). -
Find the initialization value. Usually, we start from divergence side.
The difficulty of DP is how to define optimal subproblems. We will introduce some techniques to define subproblems. Almost every question can be resolved recursively, but not all questions can be resolved iteratively.
Problems
Matrix Type:
If the question offers a matrix as input, and it is not finding the shortest path or finding the shortest path but with weights not always 1, we shall think of using DP. Matrix can be consider as a graph, the node will be each cell, and its neighbours will be its surrounding cells, which also means a cell and its surrounding cells are connected. For the matrix type DP, we shall think of how to transit the states from its neighbours to the cell.
个人总结了一个小技巧,Matrix Type question, 不像sub sequence type,一般不会根据不同的choice选择用不同元素的subproblem的答案来组成新的problem。所有用来组成新答案的元素的结果通常就是我们recursion function里要用的子问题的结果。所以Matrix Type的子问题比较好找。找到这些元素后,我们可以用例子,自己算一遍每一个位置的结果,并找到每个新元素与其前面用的元素的结果的关系。从两头推导, 更容易找到recursion function。
LeetCode 62. Unique Paths
LeetCode 63. Unique Paths II
LC 64. Minimum Path Sum
LC 221. Maximal Square
516 Paint House II
Sub Sequence Type:
Im mathematic, a subsequence is a sequence that can be derived from another sequence by deleting some or no elements without changing the order of the remaining elements. For example, the sequence {A, B, D} is a subsequence of {A, B, C, D, E, F} obtained after removal of elements E, and F . If a question requires to find a value of some elements in a sequence and the elements’ orders are fixed but not necessarily consecutive, we shall consider the question as DP sub sequence problem.
The sub sequence type’s recursion function is harder to define. It is not like matrix type’s question, the subproblem’s elements are sometimes hard to find. Basically, depends on different choices, we will decide which elements’ result will be used in the recursion function.
DP’s definition usually is what the question asks among all subsequences ending or starting with ith element. Here, ending or starting with ithelement doesn’t mean to the ith element has to be presented.
To recursively enumerate all sub sequences, we have two different ways.
-
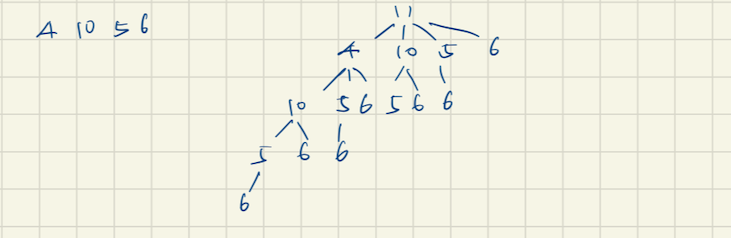
One is discontinuously enumerating all elements. Starting from each element horizontally, we will enumerate all possible elements after the starting element in the next line. Such way, line by line, we will finish enumeration by reaching to the last element. We can use this way for all sub sequence questions.This way is usually used for one dimensional DP functions, which means each element only has one state, used or not in the final result.
Following are some techniques to derived the recursion function from discontinuous decision tree,
- Elements on the last level are all possible initial special case.
- We usually get the result from the bottom to the top.
- To find the optimal sub problems, the elements which we have calculated from the lower level won’t be calculated any more.
- The recursion function shall cover all cases between every two level. If the lower level’s index has no pattern to induced the upper level, we shall scan all possible indexes in the lower level.
- The result shall be above all levels, which is “()” in the diagram
The decision tree is as below,
-
Second is continuously enumerating all elements. For each element, we have 2 choices, present or not. Each level will only have one elements present or not. This way is usually used for 2-dimensional DP functions. Here we need to notice that not all one-dimensional DP functions can be derived from this method. If an element’s DP result depends on its former
<= 2DP results and the former 2 results between every 2 level are relatively fixed, we can use this way.Following are some techniques to derived the recursion function from continuous decision tree,
-
We often collect all DP results along bottom-up direction. The meaning is starting from the current level’s element to the end result.
-
We can often find recursion function from the minimal structure of two closet present elements. For example, here two closest elements can be
4and10. -
From a present element to non-present element, we will describe non-present element as
dp[i + 1]and the present element asdp[i]. -
From a non-present element to a present element, we need to find its closed upper present element, and update the upper present element
ithresult by calcuating theithelement and the non-presentjresult, such asdp[i] = {nums[i] + dp[j], ...}. -
From a present to a present element, we need to update the upper present element
ithresult by calculating theithelement and the present(i + 1)thelement’s result, such asdp[i]= {nums[i] + dp[i + 1], ...} -
From a non-present element to a non-present element, we will use the closed to the upper number’s result. Since the result can be passed on along the bottom-up direction among all non-present elements.
-
If there is a branch, we need to compare the result and choose one of them.
The decision tree is as below,
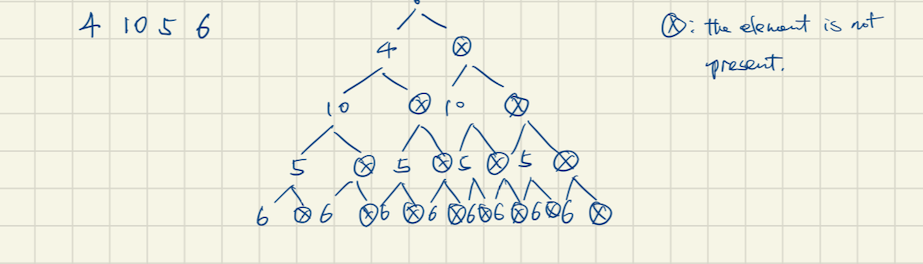
-
LC 198. House Robber
LC 213. House Robber II
LC 300. Longest Increasing Subsequence
121. Best Time to Buy and Sell Stock
122. Best Time to Buy and Sell Stock II
1911. Maximum Alternating Subsequence Sum
Continuous Segment Type:
The continuous segment type questions usually offer a sequence. We can split the sequence into several segments and every segment needs to satisfy some requirements. The number of segments can be fixed as k, or not fixed. To resolve this type of question,
- This type of question,
dp[i]usually means length ofi’s ‘ result. To include all length, and DP index starts from0, we often definedp.lengthaslength + 1 - We need to find what elements’ results will be used in the recursion function. The elements are usually defined as any element before
iwhich can formilength result. Usually those elements combine with one satisfied segement will formIlength result . - Calculate those element’s results, and use them to find the pattern between the
ithelement’s result and all other former element’s result. - Write the DP function.
279. Perfect Squares
139. Word Break
132. Palindrome Partitioning II
437 Copy Books
Two Sub Sequences Type:
This type of question’s input is usually two strings. Some sample questions are as following,
- Questions about whether two strings can match with each other by following some patterns.
- Questions about whether one string includes the other string.
- Questions about whether one string can change to the other string by following some changing rules.
- Questions about the two strings’ common subsequences
- ….
Those questions usually use 2D array to save DP result. dp[i][j]usually represents str(0...i), and str(0...j)’s result. Those questions usually include empty string’s situation. Therefore, the result array length is usually input string’s length + 1. The best way to find the recursion function is to find from its 2D result table.
LC 1143. Longest Common Subsequence
72. Edit Distance
97. Interleaving String
Knapsack Type:
Knapsack Problem is a typical DP question, and Its input is easily distinguished. The problem offers a sum, and a weight array whose element value can be a part of sum, as inputs. Sometimes, it offers another cost array whose element’s index same as weight array. The Knapsack problem’s subproblem is in 2D dimension. One dimension is sum from 0 to the total result. Another dimension is index of weight array. Since weight array and cost array own the same index, we can find its cost easily as well.
The Knapsack problem’s recursion function is short and easy to remember. Here we will draw the result diagram and find the recursion function first. Latter, we can remember the function and directly use it.
01 Knapsack:
Here we will use an example to find the pattern. Suppose our sum is 10, the weight array is [2, 3, 5, 7], and the cost array is [2, 5, 2, 5]. The 2D array is one dimension is from 0 to 10, and another dimension is input two arrays’ index. Following are the result table,

From the table, we can find the recursion function as dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - w[i]] + c[i]])
Unbounded Knapsack:
If every element in weight array can be used multiple times, the problem becomes complete Knapsack problem. We will use the same example and find its recursion function.
First we will draw the result table,

The recursion function will be as dp[i][j] = max(dp[i - 1][j], dp[i][j - w[i]] + c[i]])
Both knapsack problems’ recursion function have meanings, the meaning explanation can be found from blog Labuladong Blog. Here we only need to remember the recursion function and how they are derived.
92 Backpack
125 Backpack II
440 · Backpack III
562 Backpack IV
416 Partition Equal Subset Sum
322. Coin Change
518. Coin Change 2
89 · k Sum
Interval Type:
Those questions need to make choice from both ends of input, or to delete elements from middle. Those questions are easier to resolved by DFS + memorization, because their DP results are traversed along diagonal direction. As matrix property, diagonal index’s sum are always be the same, which is the length of input. If we need to traverse along diagonal, we will use this property. Since the recursion function is hard to find for those questions already, we will not use diagonal traverse way, but DFS + memorization.
516. Longest Palindromic Subsequence
312. Burst Balloons
This article is inspired from the following articles,