Depth First Search Dfs

Depth First Search is traversing through a multiple-branch decision tree. The question usually requires all solutions. Since DFS time complexity is O(2^n) or O(n!), tree’s depth can not be very big. DFS is often used to resolve Combination and Permutation problems.

Basic Knowledge:

DFS problem has a template. As long as you can draw the decision tree, you can resolve the issue by the template. Here is the template, modified from labuladong

result = []
def dfs(choice, choice list):
    
    if satisfied the requirment:
        result.add(choice)
        return

    for choice in choice list:
        make the choice
        dfs(choice, choice list)
        cancle the choice

The main issue that DFS can resolve is to enumerate all combinations or permutations of some data. The combination and permutation decision tree look a bit different. As well, their way of keeping track of choice list are different too.

Combination:

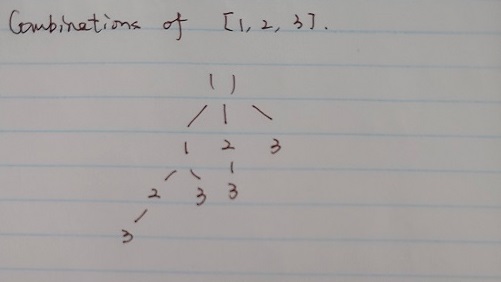
Permutation:

Combination decision tree has more nodes on the left side than on the right side. Permutation decision tree are equally distributed on the left and right side.

Combination DFS template:

Most of base cases are explicitly shown as in what situation the program will exit, that is, when the program doesn’t need to call recursion. However, this template did not show the exiting situation, instead, it shows in what situation program needs to call the recursion.

Combination uses start index to exclude choices before the index you are choosing

result = []
def dfs(nums, startIndex, subset, result):
		
	result.add(subset)
    
    for(int i = startIndex; i < nums.length; i++)
    	subset.add(nums[i]);
    	dfs(nums, i++, subset, result);
    	subset.removeLast();

Permutation DFS template:

Permutation uses a visited array to exclude choices has been chosen before.

result = []
def dfs(nums, boolean[] visited, subset, result):
    if satisfied the requirment:
        result.add(subset);
        return

    for(int i = 0; i < nums.length; i++) 
    	if(visited[i]) {
    		continue;
    	}
    	subset.add(nums[i]);
    	visited[i] = true;
    	dfs(nums, visited, subset, result);
    	subset.removeLast();
    	visited[i] = false;
    

If there are duplicates in permutation or combination, we only choose the duplicates once, that is to say, if we met the duplicate number second time, we won’t choose the duplicate number, neither call further recursion. The combination or permutation duplicates will exclude some choices from the original template. The decision trees for duplicate numbers are as followings,

Combination with duplicates(After sorting, the same element appears more than once):

Permutation with duplicates:

We shall draw the decision tree. the tree’s horizontal enumeration will be one position’s all possibilities. The vertical enumeration will be one solution.
We shall tell the question is a combination or a permutation problem. If a result’s member changes its order and the result will count as another solution, it is a permutation problem. Otherwise, it is a combination problem.
The enumeration varies in different ways. It is not necessary always from 0 to n. It can be 4 directions of a point, neighbors of a node, and so on. The loop inside dfs will help to enumerate all possibilities.
The recursion can control the vertically loop by call another dfs or return. The for loop can control horizontally loop by conditionally call dfs recursion.

Depth First Search Dfs

Basic Knowledge:

Problems:

17. Subsets

18. Subsets II

135. Combination Sum

90. k Sum II

136. Palindrome Partitioning

680. Split String

973 1-bit and 2-bit Characters

15. Permutations

16. Permutations II

33. N-Queens

34. N-Queens II

816. Traveling Salesman Problem

427. Generate Parentheses

815. Course Schedule IV

795. 4-Way Unique Paths

425. Letter Combinations of a Phone Number

37. Sudoku Solver